Owing to this struggle for life, variations, however slight and from whatever cause proceeding, if they be in any degree profitable to the individuals of a species, in their infinitely complex relations to other organic beings and to their physical conditions of life, will tend to the preservation of such individuals, and will generally be inherited by the offspring. The offspring, also, will thus have a better chance of surviving, for, of the many individuals of any species which are periodically born, but a small number can survive. I have called this principle, by which each slight variation, if useful, is preserved, by the term Natural Selection. — Darwin, 1859 (Darwin 1859).
The standard way to design an analog amplifier is to calculate the values of its components analytically. This post shows how to automate this process and make a computer determine the values on its own — using evolutionary algorithms, namely evolution strategies, to optimize the component values of single and two-stage common-emitter amplifiers. We propose various fitness functions for evaluating the amplifiers, integrate the ngSPICE circuit simulator to simulate and assess each candidate design, and perform experiments to determine the most suitable parameters for the evolution strategies. The goal is an amplifier with the desired gain, found without any manual calculation.
Prologue
In biological evolution, species are selected depending on their relative success in surviving and reproducing within their environment and mutations play a crucial role in this process as they are the key to the adaptation of the species (Brabazon, O’Neill, and McGarraghy 2015). This concept has been used as a metaphor in computer science and it inspired the formation of a whole new area of artificial intelligence called Evolutionary Computation. This area mainly deals with an optimization problem which we discuss in the following section.
Optimization Problem
Consider the function \(f: A \to \mathbb{R}\)f: A R from a set \(A\)A to the real numbers. We are looking for an element \(x_0\)x 0 in \(A\)A such that \(f(x_0) \leq f(x)\)f(x 0) f(x) or \(f(x_0) \geq f(x)\)f(x 0) f(x) for all \(x\)x in \(A\)A (we are looking for either the global minimum or maximum of the function \(f\)f). The domain \(A\)A of \(f\)f is called the search space and the elements of \(A\)A are called candidate solutions. We will call the function \(f\)f a fitness function. A candidate solution that gives us the global maximum or minimum of the fitness function is called the optimal solution. The search space \(A\)A is usually in the form of n-dimensional Euclidean space \(\mathbb{R}^n\)R n and the function \(f\)f is also n-dimensional (Bäck 1996).
A simple approach to find the optimal solution would be to scour the whole search space and try every candidate solution. This approach will always give us the optimal solution, but the search space can be so vast that we are not able to try every candidate solution in a reasonable time.
A more sophisticated approach would be to use the technique presented in Algorithm z. The population \(P \subseteq A\)P A would be a subset of the search space \(A\)A and every individual of the population would represent one element of \(A\)A. In the context of evolutionary algorithms, the individuals can also be called chromosomes. Every loop in the algorithm represents one generation of individuals. This approach helps us to avoid those elements in the search space which wouldn’t provide any good solution, but on the other hand, finding the optimal solution is not guaranteed.
From the biological point of view, this algorithm can be seen as the driving force behind evolution and from the mathematical point of view, it can be seen as a stochastic, derivative-free numerical method for finding global extrema of functions that are too hard or impossible to find analytically.
Biology uses this approach to create well-adapted beings and humans can use this method to find optimal solutions to problems that are difficult to solve analytically.
Algorithm z. Evolutionary algorithm (Brabazon, O’Neill, and McGarraghy 2015).
- Create a population P of randomly selected candidate solutions.
- Repeat:
- (Selection) Select the appropriate individuals (parents) for breeding from P.
- (Mutation) Generate new individuals (offspring) from the parents.
- (Reproduction) Replace some or all individuals in P with the new individuals.
- Until terminating condition.
Evolution Strategies
Evolution strategies (ES) is a family of stochastic optimization algorithms that belongs to the general class of evolutionary algorithms. It was created by Rechenberg and Schwefel in the early 1960s and attracted a lot of attention due to its strong capability to solve real-valued engineering problems. ES typically uses a real-valued representation of chromosomes and the evolutionary process relies primarily on selection and mutation. ES also often implements self-adaptation of the parameters used for mutating the parents in the population during evolution, which means that these parameters coevolve with the individuals. This feature is natural within evolution strategies and other evolutionary algorithms have adopted it as well over the last years (Brabazon, O’Neill, and McGarraghy 2015) (Eiben and Smith 2003).
Algorithm q is a basic non-self-adaptive form of ES. Chromosomes in this algorithm are in the form of vectors of real numbers \(x = (x_1, \ldots, x_n) \in \mathbb{R}^n\)x = (x 1, , x n) R^n. Every vector represents one solution of the search space in our problem domain and the goal of the algorithm is to find a vector that produces the global extremum of the fitness function.
The terminating condition of the algorithm can have various forms which can be combined, for example:
- Wait until the algorithm finds a chromosome with a fitness function value that meets our requirements.
- Limit the total number of generations.
- Track the best chromosome in every generation and stop the evolution if the fitness doesn’t change after a certain number of generations.
The last two approaches are suitable when the algorithm gets stuck in a local optimum and doesn’t leave it after a significant amount of time.
Algorithm q. Non-self-adaptive \((\mu + \lambda)\)( + )-ES (Brabazon, O’Neill, and McGarraghy 2015).
- Randomly create an initial population \(\{\vec{x}^1, \ldots, \vec{x}^\mu\}\)\\vecx 1, \ldots, \vecx} \mu\} of parent vectors, where each vector \(\vec{x}^i\)x i is of the form \(\vec{x}^i = (x^i_1, \ldots, x^i_n)\)x i = (x i_1, , x^i_n), \(i = 1, \ldots, \mu\)i = 1, , .
- Evaluate the fitness function of each chromosome.
- Repeat:
- Repeat:
- Randomly select a parent from \(\{\vec{x}^i : i = 1, \ldots, \mu\}\)\\vecx i : i = 1, \ldots, \mu\.
- Create a child vector by applying a mutation operator to the parent.
- Until \(\lambda\) children are generated.
- Rank the \(\mu + \lambda\) + chromosomes (children and parents) from best to worst.
- Select the best \(\mu\) of these chromosomes to continue into the next generation.
- Repeat:
- Until terminating condition.
Selection
There are two main parameters in evolution strategies that are used to describe the type of the selection process:
- Parameter \(\mu\) specifies the number of chromosomes (parents) that are selected for reproduction.
- Parameter \(\lambda\) specifies the number of children that are produced in every generation.
There are also two types of selection:
- \((\mu + \lambda)\)( + )-ES selection scheme,
- \((\mu, \lambda)\)(, )-ES selection scheme.
In the first scheme, denoted by \((\mu + \lambda)\)( + )-ES, both parents from the previous generation and newly produced children are mixed together and compete for survival in every generation where only the best \(\mu\) chromosomes (parents for the next generation) are selected and get the chance to be reproduced. This scheme implements so-called elitism because if there is a chromosome with a very good fitness function, it will survive for many generations and it can be replaced only if a better individual occurs. This approach has a higher natural tendency to get stuck in local optima than the second scheme.
In the second type of selection, denoted \((\mu, \lambda)\)(, )-ES, the parents are selected only from the set of \(\lambda\) children, so every chromosome lives only in one generation. Even a chromosome with a very good fitness function is discarded and replaced by a child with potentially worse fitness, so the convergence is not as strict as in the previous scheme, but it is easier to move away from a local optimum for this method (Brabazon, O’Neill, and McGarraghy 2015) (Eiben and Smith 2003).
Mutation
Chromosomes in evolution strategies are represented as vectors of real values:
\[\vec{x} = (x_1, \ldots, x_n)\]
These values correspond to the solution variables. The simplest form of mutation is \(\vec{x}(t+1) = \vec{x}(t) + m\)x(t+1) = x(t) + m where \(m = N(0, \sigma)\)m = N(0, ) is a real number drawn from a normal (Gaussian) distribution with mean 0, and the standard deviation \(\sigma\) is chosen by the user. The parameter \(\sigma\) represents the mutation step size and its value is crucial since it determines the effect of the mutation operator. The value should be kept relatively small compared to the problem domain in order not to perform large mutations too often. It is also important to keep the values \((x_1, \ldots, x_n)\)(x 1, , x n) of the candidate solution in their domain interval and return it every time the mutation shifts it out of the interval.
This approach ignores two important facts:
- When the algorithm is close to the global optimum, it is appropriate to perform only subtle changes to the chromosomes so that the algorithm will not leave the good region.
- Every dimension in the solution space may require different scaling. Hence, one dimension may require large mutation steps whilst another dimension only small ones.
Both these facts proved to be crucial to the ability of the algorithm to find an optimal solution during the implementation, so they are discussed in the following sections.
Mutation with One Step Size
In this version of mutation, we change the vector \(\vec{x}\)x to \(\vec{x} = ((x_1, \ldots, x_n), \sigma)\)x = ((x 1, , x n), ), where \((x_1, \ldots, x_n)\)(x 1, , x n) is the original vector and \(\sigma\) is a real-valued strategy parameter which controls the mutation process for every chromosome separately. The mutation process is:
\[\sigma(t+1) = \sigma(t) \cdot e^{\tau \cdot N(0,1)}\] \[x_i(t+1) = x_i(t) + \sigma(t+1) \cdot N_i(0,1), \quad i = 1, \ldots, n\]
The constant \(\tau\) is set by the user and it is inversely proportional to the square root of the problem size. It represents the learning rate of the algorithm. The \(\sigma\) parameter is then mutated by multiplying with a variable with log-normal distribution, which ensures that \(\sigma\) is always positive. The reasons for this form of mutation of \(\sigma\) by a log-normal distribution are stated in (Eiben and Smith 2003). The newly mutated \(\sigma\) is then used to mutate the solution values for the child where \(i = 1, \ldots, n\)i = 1, , n are the \(n\)n elements making up one chromosome. It is important to keep the right order of the mutation — to mutate the value of \(\sigma\) first and then mutate the vector’s elements themselves.
This approach allows the mutation step size to coevolve with the chromosomes since the fitness function indirectly evaluates the suitability of the mutation. It is important to vary the step size during the evolution run as we want the algorithm to prefer longer steps when it is far away from the optimum and small steps when it is close to the optimum.
Mutation with n Step Sizes
The fitness function surface can have a different inclination in every dimension, so while one dimension requires large mutation steps, another might only require subtle ones. We can solve this problem by adding a strategy parameter \(\sigma\) to every element of the chromosome’s solution vector:
\[\vec{x} = ((x_1, \ldots, x_n), \sigma_1, \ldots, \sigma_n)\]
The mutation process is then:
\[\sigma_i(t+1) = \sigma_i(t) \cdot e^{\tau’ \cdot N(0,1)’ + \tau \cdot N_i(0,1)}\] \[x_i(t+1) = x_i(t) + \sigma_i(t+1) \cdot N(0,1)_i, \quad i = 1, \ldots, n\]
where \(\tau’ \propto 1 / \sqrt{2\sqrt{n}}\)’ 1 / 2\sqrtn and \(\tau \propto 1 / \sqrt{n}\) 1 / n. Notice that the one-step mutation differs from the n-step version because one more normally distributed variable was added to the exponent. The reason is that we want to keep the overall change of the mutability but we also want a finer granularity on the coordinate level (Brabazon, O’Neill, and McGarraghy 2015) (Eiben and Smith 2003).
Analog Amplifiers
The goal is to automate the design of analog amplifiers. These are electronic circuits that are used to increase the input signal with the minimum amount of distortion to the output signal.
Single Stage Common Emitter Amplifier
The single stage common emitter amplifier was chosen because it belongs to the most commonly used examples of analog amplifiers in class A. The circuit diagram is shown in Figure x. A thorough description of this circuit can be found in (Horowitz and Hill 2015).
Figure x. Circuit diagram for the common emitter amplifier.
Resistors \(R_1\)R 1 and \(R_2\)R 2 are used to bias transistor \(Q_1\)Q 1 in order to set the quiescent point of the transistor to the middle of its DC load line so that the collector of \(Q_1\)Q 1 is put at \(1/2\)1/2 of the supply voltage \(V_1\)V 1. This allows the maximum symmetrical swings of the output signal without clipping (flattening of the top or the bottom of the waveform). The collector voltage depends on the collector current (quiescent current), \(V_c = V_1 - I_c \cdot R_c\)V c = V 1 - I_c R_c. This current depends on the applied base bias and the values of \(R_c\)R c and \(R_e\)R e.
Instead of using a voltage divider for biasing, it is possible to use only resistor \(R_1\)R 1, but this approach would make the quiescent point highly dependent on the current gain \(\beta\) of the transistor. This parameter varies considerably in every transistor and the manufacturer usually specifies only a certain range of \(\beta\). For this reason, we use a voltage divider constituted by \(R_1\)R 1 and \(R_2\)R 2 whose impedance should be small compared with the impedance looking into the transistor base, \(R_1 \| R_2 \ll \beta R_e\)R 1 \| R 2 \ll \beta R_e. This will give us a divider which is stiff enough so that the quiescent point is insensitive to variations in transistor \(\beta\). However, the current flowing in the divider should not be unnecessarily large as it affects the overall consumption of the amplifier.
Capacitors \(C_{in}\)C in and \(C_{out}\)C out form high pass filters and they are used as coupling capacitors to separate the AC signals from the DC voltage used to set up the amplifier. Their values are chosen so that the capacitors have low impedance for the desired input and output signal frequencies. This ensures that the signal’s average is zero, as the capacitors pass only AC signals and block any DC component.
The input voltage \(V_{in}\)V in causes a wiggle in the base voltage. The emitter voltage follows the base voltage, which causes a wiggle in both the emitter and collector current. The output voltage, which is the collector voltage, depends on the current flowing through \(R_c\)R c. When this current rises, the collector voltage drops and vice versa. That means that the amplifier also inverts the input signal. The output AC signal is then superimposed on the collector DC voltage and the DC component is subsequently filtered out by the capacitor \(C_{out}\)C out (high pass filter).
Capacitor \(C_e\)C e is used to reach the amplifier’s maximum gain. The values of \(R_e\)R e and \(R_g\)R g set the emitter voltage which affects the amplifier’s gain and we usually want these values to be as low as possible since this gives us the highest gain. However, if the emitter voltage is too low, it will vary significantly as the base-emitter drop varies with temperature. The solution is to bypass the \(R_e\)R e resistor so that the impedance for the emitter will vary according to the signal’s frequency. The bypass capacitor \(C_e\)C e is an open circuit component for DC bias and the emitter voltage depends on both \(R_e\)R e and \(R_g\)R g, which allows stable biasing. For higher frequency signals, the bypass capacitor short circuits \(R_e\)R e and the emitter voltage now depends mostly on \(R_g\)R g whose value sets the maximum gain.
The analytical calculation for this circuit is left up to the evolutionary algorithms. The subjects of the optimization are elements \(R_1\)R 1, \(R_2\)R 2, \(R_e\)R e, \(R_g\)R g, \(R_c\)R c, \(C_{in}\)C in, \(C_e\)C e, and \(C_{out}\)C out. These elements represent the solution variables in the evolution strategies and make up the vector \(\vec{x}\)x. In this case, we optimize 8 components in the circuit so the search space has 8 dimensions.
Two Stage Amplifier
The circuit diagram for a two stage amplifier is shown in Figure a. The functionality and structure of the circuit are similar to the previous one. The difference is that now we use two transistors connected in a cascade where transistor \(Q_1\)Q 1 sends its output to the base of transistor \(Q_2\)Q 2. This circuit was chosen as a more difficult problem to optimize, since the structure is twice as complicated as in the previous amplifier. The subjects of the optimization are all the resistors and capacitors in the diagram apart from resistor \(R_{load}\)R load, so we have 14 components to optimize which makes the search space 14-dimensional.
Figure a. Circuit diagram for the two stage common emitter amplifier.
ngSPICE
ngSPICE is an open-source, general-purpose circuit simulation program based on SPICE (Simulation Program with Integrated Circuit Emphasis). It can simulate circuits with linear components and also nonlinear circuits that contain common semiconductor devices. Besides the simulation of analog circuits, it also offers simulation of digital circuits, in which case the simulator operates only with the logic states of the circuit, which has a great influence on the speed of the simulator. ngSPICE also offers a mixed-mode simulation where both the digital and analog simulations are combined.
ngSPICE uses a language whose syntax has been inherited from SPICE for describing circuits. An example of such a description of the circuit from Figure x is shown in Listing 9. The first line contains the name of the circuit and on the next four lines, there is a description of the transistor used in the circuit. On the next lines, there is a list of the circuit’s components. The name of the component is on the first position followed by the numbers or names of the nodes that the component is connected to. The last position contains the properties of the component. The second last line contains the description of the simulation. In this case, we do a transient analysis of the circuit for 1.22 ms with the sampling period of 20 \(\mu\)s which provides the time course of the amplifier’s output signal. Later on, we use this data to evaluate the amplifier’s quality.
Listing 9. Description of the common emitter amplifier using the SPICE syntax.
amplifier
.model bc547c NPN (BF=730 NE=1.4 ISE=29.5F IKF=80M IS=60F
+ VAF=25 ikr=12m BR=10 NC=2 VAR=10 RB=280 RE=1 RC=40
+ VJE=.48 tr=.3u tf=.5n cje=12p vje=.48 mje=.5
+ cjc=6p vjc=.7 mjc=.33 isc=47.6p kf=2f)
Vin in 0 sin(0 .1 2k)
V1 4 0 9
Ce 0 5 5u
Cout 1 out 220n
Cin in 3 220n
Rc 1 4 1k
Rload 0 out 22k
Re 0 5 1k
Rg 5 2 40
R2 0 3 33k
R1 3 4 47k
Q1 1 3 2 bc547c
.TRAN 20u 1.22m
.end
In Figure o we can see the simulation output of the circuit from Listing 9, which is the same circuit as in Figure x. This circuit was also built using real electronic components in order to verify the simulation results. The measurement results of the real circuit proved that the simulator works correctly for this circuit as the measured values corresponded to the simulation.
Figure o. Simulation of the single stage common emitter amplifier.
The last version of ngSPICE offers a C API, which makes the simulator the ideal choice for utilizing it with the evolutionary algorithms. Every chromosome (candidate solution) in the evolution represents one amplifier and the simulator is used to determine its quality.
The API is used to pass the description of the amplifier to the simulator, run the simulation and obtain the simulation results. The results are in the form of arrays in C that represent time and the corresponding voltage values. These arrays have an equal length which depends on the simulation duration and the sampling period.
The default input frequency for the amplifier is 2 kHz, the duration of the simulation is set to 1.22 ms and it contains approximately two and a half periods of the output signal. The duration does not need to be longer because the shape of the waveform does not change after the circuit gets to a stable state. The sampling period is 20 \(\mu\)s so that the waveform is smooth enough and the simulation does not take too long. The array containing the output voltage is used for the evaluation of the chromosomes.
The simulator is launched several thousand times during a typical evolution and it takes most of the computation time. During the implementation of the algorithms and the integration of the simulator, it emerged that there were memory leaks in several places in the source code of the simulator. This was a problem as the simulator leaked memory in every iteration. A significant amount of time was spent on fixing these bugs and the result is that the memory leaks have been removed. These improvements were proposed as a patch to the development team and they were incorporated into the next versions of ngSPICE.
Evaluation of Amplifiers
A fitness function provides the means to determine how good the evolved solution is so that the most appropriate candidates can be distinguished from the less appropriate ones. It is important to mention that the quality of this function is essential because the ability of the algorithm to find the most suitable solution is highly dependent on the ability of the fitness function to distinguish between the individuals. In our case, the value of the function is a positive real number and the algorithm uses it only for comparing the individuals with each other. We consider individuals with a lower value to be the better ones.
The implementation required some methods of trial and error and in the end, there are three fitness functions implemented. All of them use the ngSPICE simulator in order to obtain the output of the amplifier and assess it afterwards. The simulation is done for every candidate solution and it takes most of the computation time of the overall evolutionary algorithm.
Best Match with the Reference Solution
This fitness function was implemented as the first one in order to find out if the evolution has at least the ability to get close to the analytical solution. It is based on the method of least squares which is used in regression analysis.
The fitness function uses the output voltage vector from the simulator for assessing the chromosomes. The vector represents the waveform of the output signal from the circuit and the shape of the waveform gets similar to an inverted sine wave as the solution evolves. The length of the vector is set to 69 (the sampling period is approximately 20 \(\mu\)s) elements during the whole evolution and the vector contains approximately 2.5 periods of the signal. The fitness function uses two types of these vectors, one serves as the reference vector (the output of the amplifier whose component values were calculated analytically) and all the candidate vectors are compared to it. As we can see in Figure o, the first period of the signal is unstable, so the fitness function skips it and picks only the second period for comparison with the reference signal. It is sufficient to compare only the second period because the shape of the signal doesn’t change anymore after the circuit gets to a stable state.
The function iterates over the second period in both reference and candidate vectors and calculates the sum of squares defined by the difference between the values in the reference vector and the candidate vector:
\[\text{fitness} = \sum_{i=\text{start}}^{\text{end}} (\text{referenceVector}[i] - \text{candidateVector}[i])^2\]
The overall sum is returned as the result of the fitness function and the lower the value, the better the candidate solution is.
The reason why we add up squares and not only the absolute values of the differences is important. Consider two imaginary vectors of two values that differ from the reference vector by \((1, 5)\)(1, 5) and by \((3, 3)\)(3, 3). The sum of the absolute values is 6 in both cases, so this method doesn’t distinguish between these vectors. However, the sum of the squares is 26 for the first vector and 18 for the second one. This difference is important as we want all the values to be close to the reference and not only some of them and therefore the second vector is assessed as the better one.
We can see the result of the evolution using this fitness function in Figure 3.
Figure 3. The result of evolution towards the analytical solution.
Ideal Sine Wave
This method is similar to the previous one but instead of using the pre-simulated output as a reference, it uses an analytically calculated sine wave. An analytical sine wave is used to force the evolution towards such a solution that won’t produce a distorted output signal since the input is in the form of a sine wave as well. The function also uses the method of least squares and it iterates over the second period of the signal.
In every iteration, it calculates the value of the sine wave and compares it with the simulated signal:
\[\text{refSine} = -\text{amplitude} \cdot \sin\left(\frac{2\pi i}{\text{refSineSize} - 1}\right)\] \[\text{fitness} = \sum_{i=0}^{\text{refSineSize}} (\text{refSine} - \text{candidateVector}[\text{start} + i])^2\]
The sum of the comparisons is then returned as the fitness value and the lower the result is, the closer the candidate solution is to the reference. The amplitude of the sine wave is set by the user, so this method allows users to design amplifiers with an arbitrary amplification which doesn’t exceed the circuit’s capabilities.
Maximal Amplitude
This fitness function is designed to rate the candidate solutions only according to the amplitude of the output regardless of the waveform’s shape. It can be used for finding the highest amplification capabilities of the circuit. The function finds the trough and the peak in the second period and returns the multiplicative inverse of their difference:
\[\text{fitness} = \frac{1}{\text{peak} - \text{trough}}\]
Waveform Symmetry
All of the fitness functions discussed above have difficulties in finding symmetrical waveforms. An example is shown in Figure t.
Figure t. An asymmetrical result of the evolution using the ideal sine wave evaluation.
The problem is that at the start, the output signal has zero power and as the evolution continues, only one half of the signal rises and the fitness function value decreases even though the evolution doesn’t go in the right direction. At the end, the evolution ends up in the state shown in Figure t. The first solution to this problem is:
\[\text{result} = (|\text{peak} + \text{trough}| + 1) \cdot \text{fitness}\]
The peak and trough values are obtained in the same way as in the maximal amplitude method. If the signal is symmetrical, the absolute value of the sum of these values is close to zero and therefore the result will also be lower. We add 1 to the sum because we need to distinguish between perfectly symmetrical signals with different fitness. However, it emerged that this approach is too restrictive as it promotes only signals that are perfectly symmetrical but often distorted. The result is shown in Figure 4.
Figure 4. A distorted result using the ideal sine wave evaluation with perfect symmetry.
The ability of the evolution to find the desired solution was also decreased because some asymmetrical candidate solutions headed towards a good solution. These consequences led to another solution to this problem. The following condition is used to separate the symmetrical and asymmetrical chromosomes:
\[\frac{\min(|\text{trough}|, \text{peak})}{\max(|\text{trough}|, \text{peak})} < 1 - \frac{\text{maxDifference}}{100}\]
The value of maxDifference is in the interval \(]0, 100]\)]0, 100] and it is set by the user. It represents the maximal percentage difference between the peak and trough in the second period of the signal. The algorithm calculates the ratio between the peak and trough and if the result is less than the threshold value, the chromosome is evaluated with the maximal fitness and the function is terminated. Otherwise, the evaluation continues. This allows the user to control the results of the evolution with respect to the symmetry of the output signal.
Experiments
The evolutionary algorithms were implemented in C++. This language was chosen due to its flexibility, performance and the possibility to make use of the ngSPICE simulator. The implementation also utilizes the RInside library, which integrates R into C++. The R language is used to plot graphs dynamically during the evolution either to the screen or to a file so the user can see and record how the solution evolves.
The program is written as a console application and the user can specify the properties of the evolution via command-line arguments. This approach also allows the user to easily run the application multiple times and collect the results of the evolution.
Initial Stages of Experiments
The first experiments were performed only in order to optimize the value of resistor \(R_1\)R 1 in the single stage amplifier. The best match evaluation method and mutations with one step size were used. The evolution always found a value close to 50 k\(\Omega\), which was the desired solution. These experiments were always successful as this was a very simple task for the evolution.
In the next stage, the task was to optimize the voltage divider constituted by \(R_1\)R 1 and \(R_2\)R 2. The best match method and mutations with one step size were used again and it emerged that the evolution was able to find the solution even faster than in the previous case. This was because we were looking only for the right ratio between the resistors and not for specific values so the set of the desired solutions was much larger in this case even though the search space was larger as well as it was two-dimensional.
The next task for the evolution was to find the right values for resistors \(R_1\)R 1, \(R_2\)R 2 and \(R_g\)R g. The evolution parameters were set in the same way as in the previous experiments. This task showed the weak spot of mutations with one step size as the evolution was able to find an acceptable solution very rarely. The reason was that the desired value of \(R_g\)R g is very close to the lower bound of the search space (the analytical value is only 40 \(\Omega\)). Since mutations with one step size use the same mutation value in every dimension, it was not possible to mutate \(R_g\)R g only by a few ohms (not to move away from the lower bound of this dimension) and at the same time look for the right values in other dimensions, which required steps in kiloohms. The value of \(R_g\)R g heavily influences the overall fitness of the chromosome because high values significantly decrease the gain of the amplifier. The usual course of the evolution was that the value of \(R_g\)R g converged quickly to the lower boundary and since this parameter has a great influence on the fitness, the evolution preferred chromosomes with this property. This led to a quick decrease of the mutation step size \(\sigma\) (the fitness function also indirectly evaluates the value of \(\sigma\)) and the algorithm got stuck in a local optimum since other dimensions (values of other resistors) in the search space could not be searched properly. The solution to this problem was to implement mutations with n step sizes. This approach allows us to treat every dimension separately and therefore search the search space more effectively. After the implementation, the evolution was able to find a satisfactory solution in most of its runs.
The previous experiments proved that the evolutionary algorithms are able to provide acceptable solutions in the domain of analog amplifiers. The next section describes the process of determining the ideal parameters for the evolution.
Evolution Parameters
In order to make the evolution strategies work efficiently, we need to find and set the correct parameters for the evolution.
The size of the search space is defined by the number of dimensions and by the size of every dimension. The number of dimensions depends on the number of electronic components that we want to optimize and the sizes of the dimensions depend on the range of the values that every component can have. These ranges were set from 0 to 200 k\(\Omega\) for resistors and from 0 to 500 \(\mu\)F for capacitors. The upper bounds are based on the values of real electronic components so, for example, we do not expect to have a higher resistance than 200 k\(\Omega\) in the circuit. The values of some particular components could have a smaller range, for example, resistor \(R_g\)R g whose value does not need to be higher than a few kiloohms, but the assumption is that we have no knowledge about the circuit at all.
The initial mutation step size \(\sigma\) is set to 100. This value is not very important because this parameter is adapted during the evolution. Experiments showed that there is no difference between setting the initial \(\sigma\) to 10 or 500 for example. However, if we set the initial value too high (10000 and above), it is more likely that the evolution will get stuck in a local optimum because the algorithm converges too quickly at the start.
The experiments also showed that the values of the learning parameters \(\tau\) and \(\tau’\)’ have a significant impact on the speed at which the evolution converges to the optimum. The higher the values were, the faster the evolution converged; nevertheless, this also means that the probability of finding only a local optimum was rapidly increased. For this reason, the values were set to \(\tau = 1 / \sqrt{n}\) = 1 / n and \(\tau’ = 1 / \sqrt{2\sqrt{n}}\)’ = 1 / 2n, their lowest possible values. The parameter \(n\)n is the number of dimensions of the search space.
The maximum difference between the peak and trough of the amplifier’s output waveform was empirically set to 25. This means that the values of the peak and trough of the waveform can differ at most by 25%.
Population Size, Selection Type and Selective Pressure
Important parameters of the evolution are numbers \(\mu\) and \(\lambda\) which define the population size (the number of parents and children in every generation) and the selective pressure which is defined by the ratio between \(\mu\) and \(\lambda\). The next important parameter is the type of the selection that we choose for the evolution (\((\mu, \lambda)\)(, )-ES or \((\mu + \lambda)\)( + )-ES). In order to determine the most suitable values of the parameters, there were various experiments carried out which are summarized in Table 5.
Every row of the table contains results for a different combination of \(\mu\) and \(\lambda\). The values of \(\mu\) are set to 1, 5, 10, and 15 and the selective pressure is also 1, 5, 10, and 15 for every value of \(\mu\), so there are four different values of \(\lambda\) for every \(\mu\). For every such combination, there are results for both selection types and under every type, there are three columns representing all the three evaluation methods. One cell of the table corresponds to the result of one experiment where the evolutionary algorithm was run 10 times with the same parameters and the fitness values of the resulting chromosomes were added up and divided by 10. The task was to optimize the single stage amplifier.
We can see that there is no significant difference between the selection schemes, provided the selective pressure is higher than one. On lines 5, 9, and 13 (where the selective pressure is 1), the \((\mu, \lambda)\)(, )-ES scheme performs significantly worse than the \((\mu + \lambda)\)( + )-ES scheme and even increasing the population size has no effect. However, when we sum up all the values in both schemes (excluding lines 1, 5, 9, and 13), the latter one gives us better results, so the \((\mu + \lambda)\)( + )-ES selection scheme was chosen as the more effective one.
We can also see that when the value of \(\mu\) is only 1, the algorithm’s results are substantially worse than in the rest of the table and on the other hand when we increase it from 5 to 15, there is only a small change in the overall performance.
The value of \(\lambda\) is set according to the value of \(\mu\) multiplied by the selection pressure and it highly influences the overall computation time of the algorithm because it defines the number of chromosomes that have to be evaluated in every generation (the evaluation includes the amplifier’s simulation which takes most of the computation time). When the selective pressure and the value of \(\mu\) are higher than one, the overall efficiency of the algorithm does not increase rapidly but there is a noticeable increase in the computation time. For this reason, the values of \(\mu\) and \(\lambda\) were set to \(\mu = 15\) = 15 and \(\lambda = 150\) = 150 as a compromise between the algorithm’s time demands and the optimization efficiency. Higher values were also examined but they did not provide any significant improvements.
Table 5. Results of experiments. Cells contain the average fitness of 10 evolution runs.
| \(\mu\) | \(\lambda\) | \((\mu, \lambda)\)(, )-ES | \((\mu + \lambda)\)( + )-ES | |||||
|---|---|---|---|---|---|---|---|---|
| best match | ideal sine | max. ampl. | best match | ideal sine | max. ampl. | |||
| 1 | 1 | 1 | N/A | N/A | N/A | 21.82 | 99.00 | 2.90 |
| 2 | 1 | 5 | 20.82 | 113.75 | 1.98 | 13.44 | 57.91 | 2.69 |
| 3 | 1 | 10 | 18.84 | 76.81 | 1.40 | 24.70 | 75.01 | 2.84 |
| 4 | 1 | 15 | 18.43 | 128.75 | 2.26 | 19.52 | 34.11 | 1.02 |
| 5 | 5 | 5 | 49.62 | 169.02 | 36.50 | 9.81 | 56.61 | 3.18 |
| 6 | 5 | 25 | 7.28 | 55.00 | 3.12 | 12.12 | 34.88 | 2.72 |
| 7 | 5 | 50 | 16.18 | 64.22 | 3.21 | 9.75 | 43.73 | 3.57 |
| 8 | 5 | 75 | 3.70 | 58.82 | 3.10 | 4.20 | 38.84 | 3.52 |
| 9 | 10 | 10 | 49.41 | 154.66 | 26.40 | 8.94 | 53.77 | 3.18 |
| 10 | 10 | 50 | 9.09 | 60.93 | 2.68 | 7.02 | 45.04 | 3.58 |
| 11 | 10 | 100 | 6.97 | 38.02 | 3.16 | 4.91 | 26.06 | 3.10 |
| 12 | 10 | 150 | 8.06 | 25.54 | 3.10 | 2.52 | 23.07 | 3.07 |
| 13 | 15 | 15 | 44.48 | 165.76 | 34.99 | 2.54 | 47.69 | 3.18 |
| 14 | 15 | 75 | 4.64 | 56.18 | 2.25 | 4.96 | 51.74 | 3.56 |
| 15 | 15 | 150 | 6.63 | 47.32 | 3.52 | 6.36 | 12.19 | 1.60 |
| 16 | 15 | 225 | 7.56 | 31.17 | 2.65 | 0.70 | 19.31 | 1.08 |
All the evolution parameters discussed above are summarized in Table 1. These parameters were chosen as the most appropriate ones.
Table 1. Optimal evolution parameters.
| Parameter | Value |
|---|---|
| Resistance range | 0–200 k\(\Omega\) |
| Capacitance range | 0–500 \(\mu\)F |
| Initial \(\sigma\) | 100 |
| Max. peak-trough difference | 25% |
| \(\mu\) | 15 |
| \(\lambda\) | 150 |
| Selection type | \((\mu + \lambda)\)( + )-ES |
| \(\tau\) | \(1 / \sqrt{n}\)1 / n |
| \(\tau’\)’ | \(1 / \sqrt{2\sqrt{n}}\)1 / 2n |
The Typical Course of the Evolution
Figure s shows the typical course of the evolution. The population size parameters were set to \(\mu = 10\) = 10 and \(\lambda = 100\) = 100 and the terminating condition of the algorithm was that the evolution ends when the value of the fitness function of the best chromosome does not decrease by more than 1% after 300 generations.
The green line represents the fitness of the best chromosome (the one with the lowest fitness) in every generation, the blue line is the fitness of the worst chromosome and the red line is the average fitness of every generation. In this case, we pick the chromosomes only from the set of \(\mu\) parents. We can see that the red line is very close to the green line so the average fitness of every generation is close to the fitness of the best chromosome and that the blue line is scattered above the other two lines.
The evolution was stuck in a local optimum for approximately 20 generations between the 80th and 100th generation and the solution was evolved approximately after 300 generations. When the blue line is close to the other two lines, it means that the sizes of the mutation steps \(\sigma\) are low and the algorithm searches only a small area of the search space. When the values of \(\sigma\) are low (close to zero), we can stop the algorithm after a few hundred generations because it will not provide any better solution than the current one and the resulting fitness is either in a local or global optimum.
The number of generations needed for the optimization is usually a few hundred. When the size of the population is low (for example \(\mu = 1\) = 1 and \(\lambda = 5\) = 5), the optimization takes a few thousand generations. In any case, there are approximately up to 30000 simulations in every evolution run which takes a few minutes (usually between two to four minutes) on the Intel Core i5-5200U processor.
In this case, the evaluation method was the best match method and this evolution run was successful since the resulting fitness was very close to zero. With this method, we can consider those solutions whose fitness is under 0.5 as sufficient because the amplifier’s output waveform is very close to the desired one. The resulting value of the fitness of the best chromosome was 0.19.
Figure s. The typical course of the evolution.
Figure u shows how the output waveform evolves across generations.
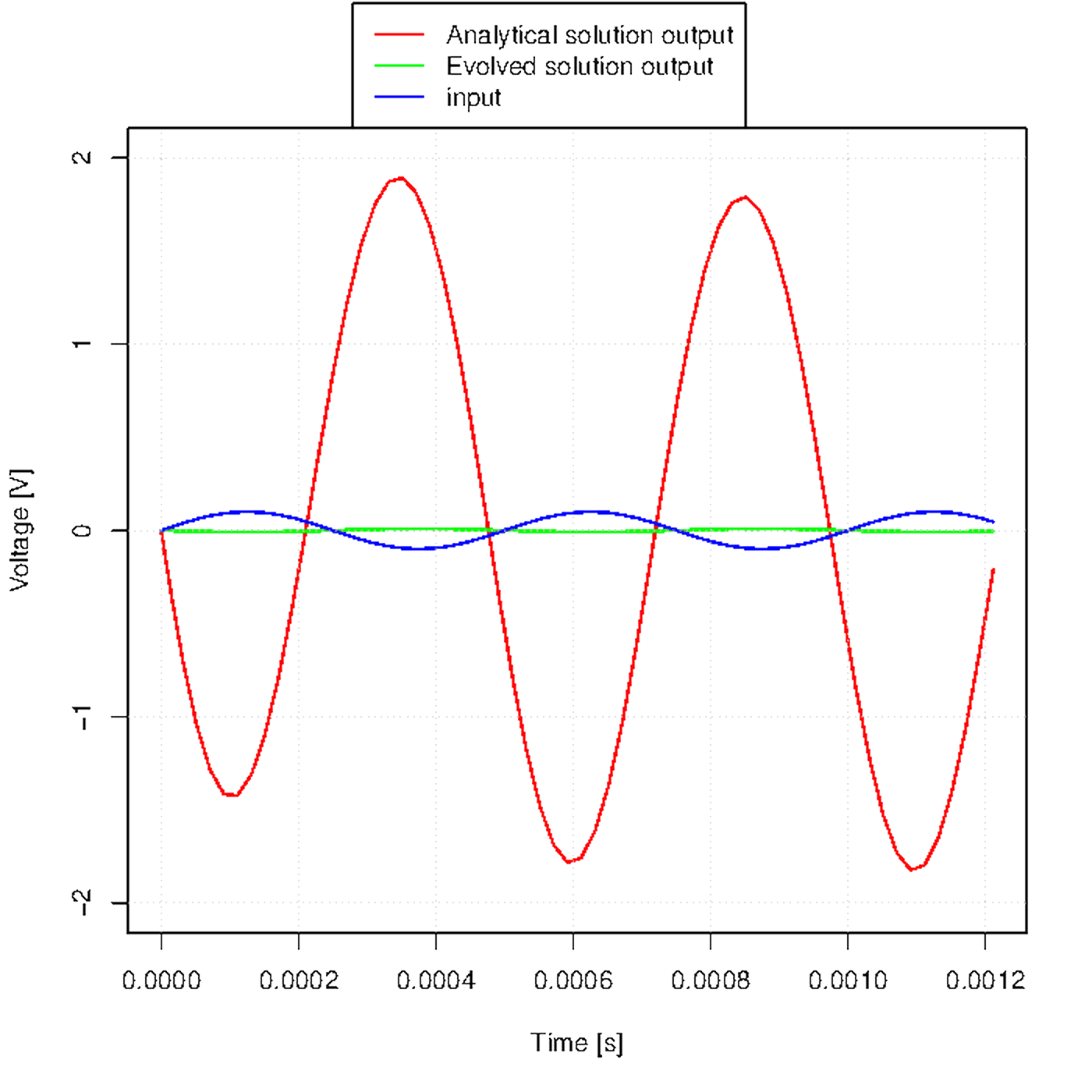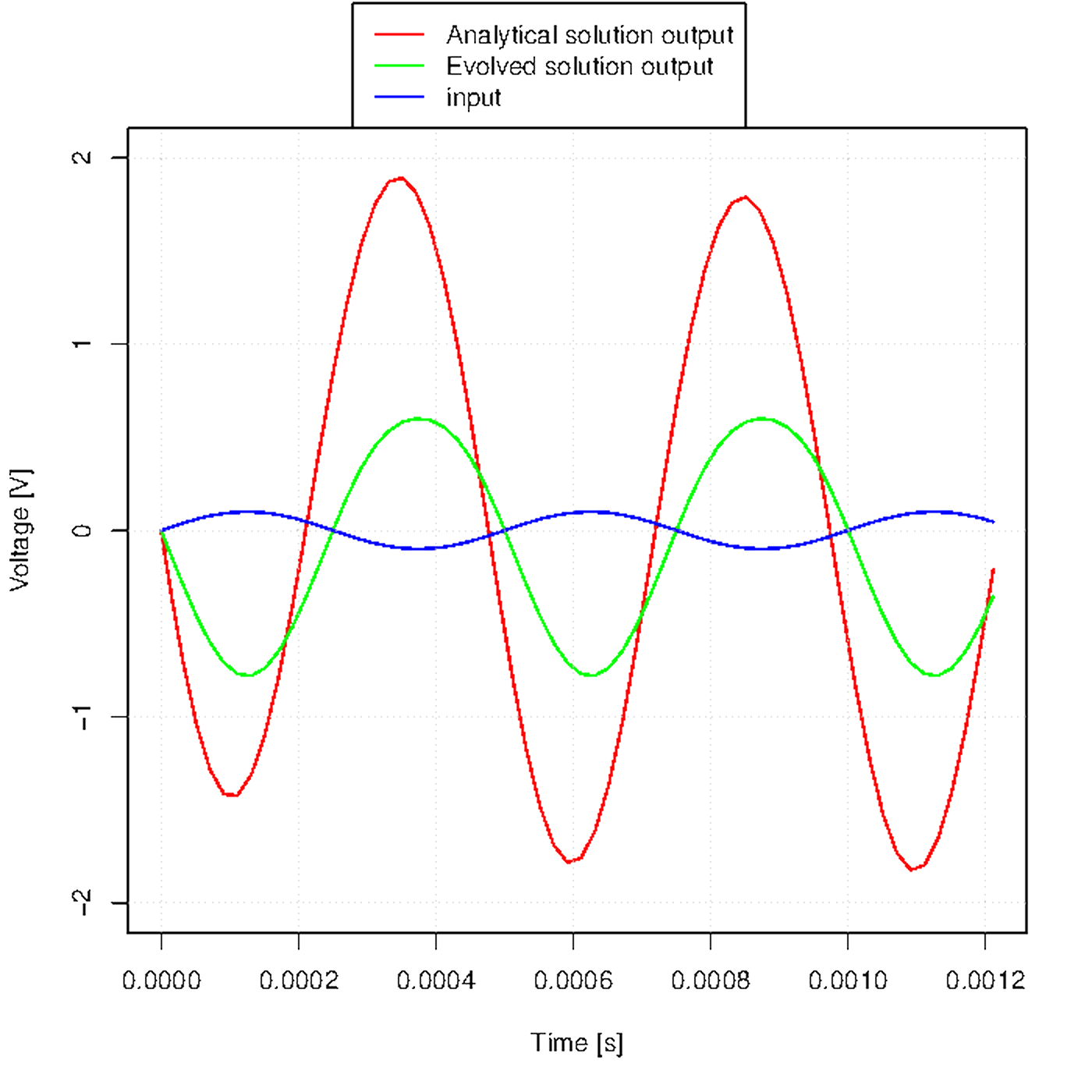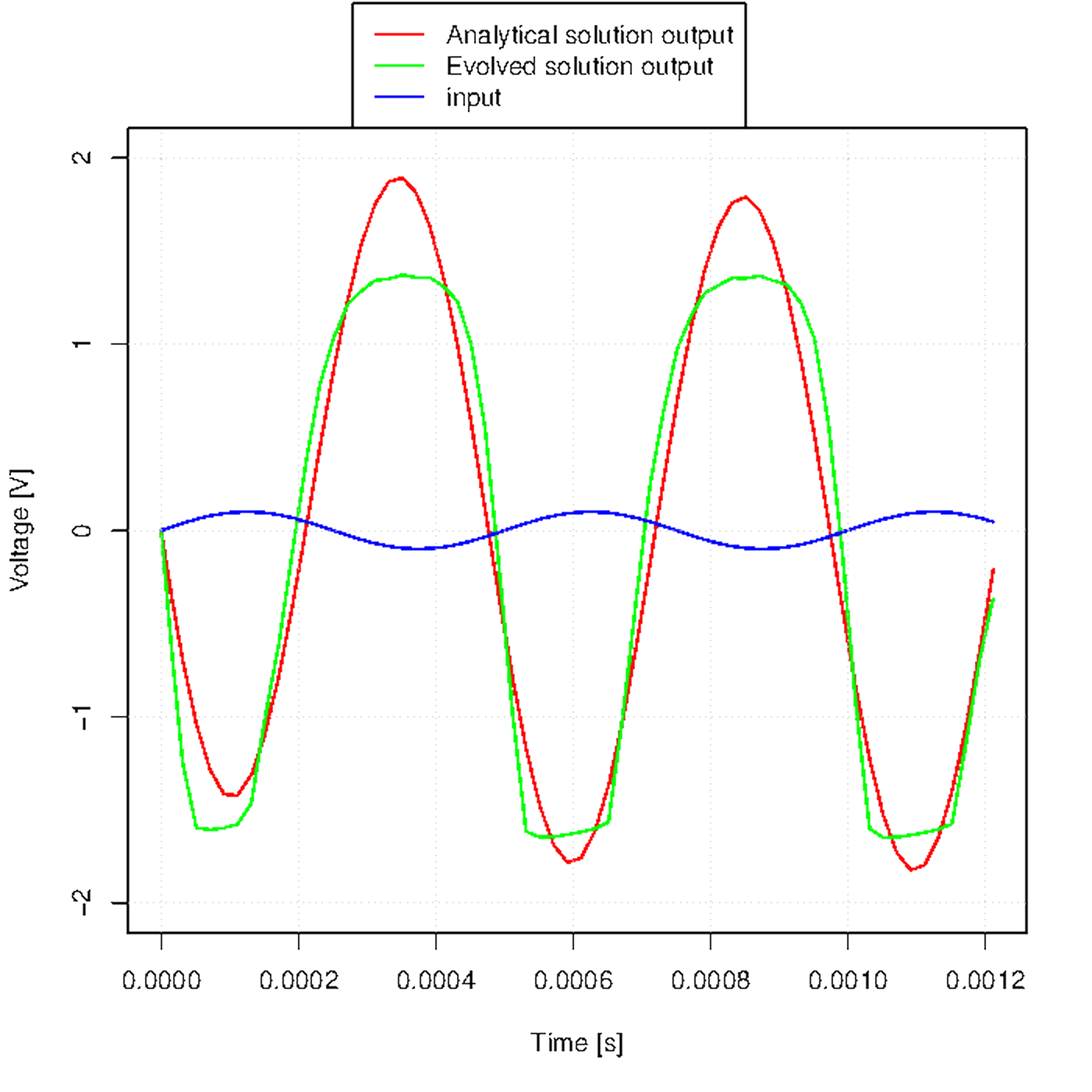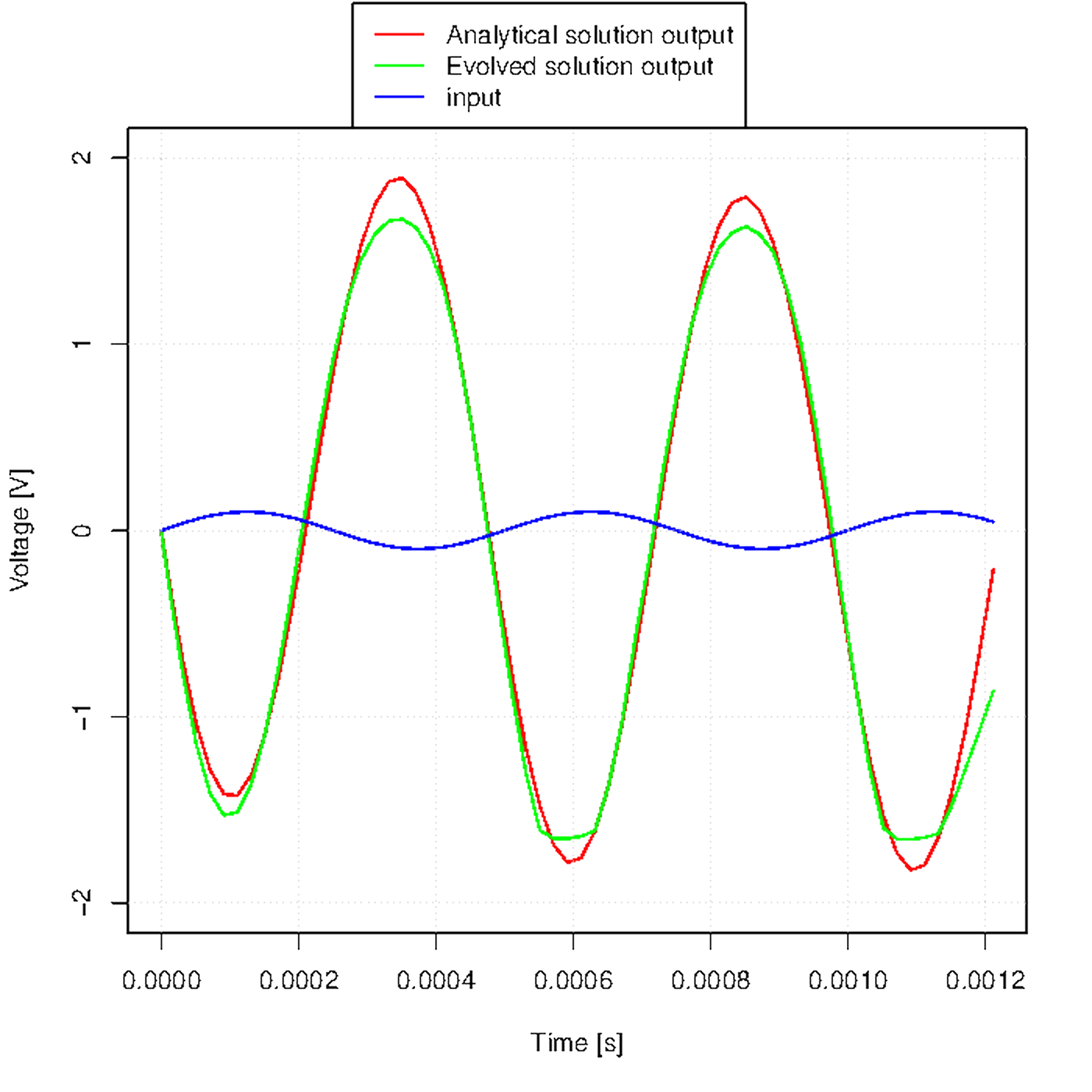 Figure u. Evolution of the output waveform across generations.
Figure u. Evolution of the output waveform across generations.
Single Stage Amplifier Optimization
Every evaluation method implemented provides different means by which we can optimize the circuit.
The best match method can be used for finding such properties that provide the most similar output compared to the analytical solution. We optimize the values of 8 electronic components and experiments with this method proved that there are many other possible combinations that provide almost identical behaviour of the amplifier. Five examples are shown in Table h. The simulation output of the amplifier with these values of components was visually identical to the analytical solution.
Table h. Values of components that provide visually identical outputs with the analytical solution.
| \(R_1\)R 1 [k\(\Omega\)] | \(R_2\)R 2 [k\(\Omega\)] | \(R_e\)R e [\(\Omega\)] | \(R_g\)R g [\(\Omega\)] | \(R_c\)R c [k\(\Omega\)] | \(C_e\)C e [nF] | \(C_{in}\)C in [nF] | \(C_{out}\)C out [nF] |
|---|---|---|---|---|---|---|---|
| 200 | 76.2 | 7510 | 471 | 21.7 | 460 | 29 | 1010 |
| 78.5 | 16 | 3370 | 429 | 23 | 228000 | 17 | 396000 |
| 141 | 11.5 | 180 | 483 | 21.1 | 285000 | 21 | 280000 |
| 82.3 | 44.3 | 8590 | 400 | 16 | 499 | 202 | 95 |
| 118 | 41.2 | 11500 | 559 | 35.4 | 419 | 95 | 19 |
The maximal amplitude method can be used for finding the best amplification capabilities of the circuit as it does not take into consideration the shape of the output signal. This method is useful for the ideal sine method because it allows us to find the appropriate maximal amplitude and then we can find the right waveform by using the latter method. By this approach, we can find even better solutions than the analytical one. One such solution is shown in Figure w and the values of the components are summarized in Table i. Since the amplitude of the input signal was \(V_{in} = 100\)V in = 100 mV and the amplitude of the output signal is approximately 4.2 V, the gain of this amplifier is approximately 42 (the gain of the analytically solved amplifier is approximately 18). The gain also depends on the voltage \(V_1\)V 1 that supplies the amplifier, which is set to \(V_1 = 12\)V 1 = 12 V in the experiments.
Figure w. The best solution for the single stage amplifier found by the evolution.
Table i. The best solution for the single stage amplifier found by the evolution.
| \(R_1\)R 1 [k\(\Omega\)] | \(R_2\)R 2 [k\(\Omega\)] | \(R_e\)R e [\(\Omega\)] | \(R_g\)R g [\(\Omega\)] | \(R_c\)R c [k\(\Omega\)] | \(C_e\)C e [\(\mu\)F] | \(C_{in}\)C in [\(\mu\)F] | \(C_{out}\)C out [nF] |
|---|---|---|---|---|---|---|---|
| 168 | 15.1 | 169 | 49 | 4.21 | 16 | 274 | 86 |
The ideal sine evaluation method also provides a universal tool for finding the appropriate values of components which produce an arbitrary amplification of the amplifier up to the maximal amplitude.
Two Stage Amplifier Optimization
This amplifier was chosen as the more complicated task to optimize. There was no analytical solution for this circuit so it was not possible to use the best match evaluation method. Experimenting with this type of amplifier showed that this amplifier is much more difficult to optimize and that it does not provide any better amplification properties than the previous single stage amplifier.
The same set of experiments was carried out as for the previous amplifier and one of the best solutions is shown in Figure 7.
Figure 7. The best solution for the two stage amplifier found by the evolution.
We can see that the resulting gain is approximately 50 (the amplitude of the input voltage is \(V_{in} = 100\)V in = 100 mV, the amplitude of the output voltage is approximately 5 V, the supply voltage is \(V_1 = 12\)V 1 = 12 V) but the output waveform is significantly distorted — the circuit generates a square wave. The experiments did not provide any solution that would generate a sine wave. The component values for this solution are stated in Table 6.
Table 6. The best solution for the two stage amplifier found by the evolution.
First stage:
| \(R_1\)R 1 [k\(\Omega\)] | \(R_2\)R 2 [k\(\Omega\)] | \(R_e\)R e [k\(\Omega\)] | \(R_c\)R c [k\(\Omega\)] | \(C_e\)C e [\(\mu\)F] | \(C_{in}\)C in [\(\mu\)F] | \(C_{out}\)C out [\(\mu\)F] |
|---|---|---|---|---|---|---|
| 114 | 57 | 51.6 | 81.7 | 98 | 215 | 479 |
Second stage:
| \(R_{gb}\)R gb [\(\Omega\)] | \(R_{eb}\)R eb [\(\Omega\)] | \(R_{cb}\)R cb [k\(\Omega\)] | \(R_{2b}\)R 2b [k\(\Omega\)] | \(R_{1b}\)R 1b [k\(\Omega\)] | \(C_m\)C m [\(\mu\)F] | \(C_{e2}\)C e2 [\(\mu\)F] |
|---|---|---|---|---|---|---|
| 22 | 298 | 3.37 | 9.24 | 80.5 | 351 | 139 |
Epilogue
This post showed the capabilities of evolutionary algorithms, namely evolution strategies, in the design analog amplifiers. The first phase was to implement evolution strategies and integrate them with the ngSPICE simulator. An inherent part of evolutionary algorithms is an appropriate fitness function, so the next step was to develop methods for evaluating the quality of the amplifiers.
The evolution found the desired solutions for the single stage amplifier and even discovered multiple component combinations that produce the same amplification properties. The two-stage amplifier proved much harder to optimize — the algorithm consistently converged to square-wave outputs rather than sine waves.
The choice of fitness function matters: the three methods developed here each suit different use cases, and users can pick the most appropriate one. The experiments also showed that extensions to the basic evolution strategies — particularly mutation with n step sizes — had a significant impact on the algorithm’s ability to find global optima.
The resulting application provides a tool for designing amplifiers with an arbitrary gain up to the maximum limits of the circuit without using any mathematical apparatus.
The work also contributed to the development of the ngSPICE simulator. Since the simulator runs thousands of times during a single optimization, memory leaks in its source code had to be fixed. The patches were proposed to the development team and incorporated into subsequent releases.